一、理论学习 1. 思维导图在小学数学教学中的妙用 2. 在小学数学自主学习中应用思维导图的实践策略探究 学习讨论;如何立足思维导图式教学引导学生绘制思维导图,设计思维导图模板,探索自主学习中的思维导图模板 二、案例研究 (一)课堂教学中学生绘制作品引导策略的探索 在教学“小数乘法”单元中的简便计算时,部分教师会将乘法的三大运算定律进行独立教学,并把重点放在各种形式的练习题上,反而忽略了沟通各个运算定律之间的本质联系,这样就容易导致学生只会模仿解题而无法进行自主、灵活的运用。鉴于此,教师可以运用思维导图来帮助学生厘清各个运算定律之间的联系,使学生更加深入地掌握简便运算的内涵。 首先,教师需要让学生明白无论是整数还是小数的乘法定律都包含了三种:结合律、交换律和分配律。 其次,教师可以引导学生将“乘法运算律”作为一个大点放在思维导图的最上方,并在其下方分别延伸出三大定律及其公式;然后在“交换律”和“结合律”中间用线条连接起来,并标注两者共同的特点是“改变运算顺序”,在分配律下方则标注“几个几不变”这个关键特点。这是因为分配律不仅改变了运算顺序,还转变了算式的样式。 最后,由于所有的乘法运算律的最终目的都是为了凑整,因此,教师可以引导学生在思维导图的最下方标注“凑整”二字,并延伸出最终的结果就是实现简便运算。这样一来,一幅完整的思维导图就完成了。学生在绘制的过程中进一步厘清了三者之间的关系,明确了其中的异同,加深了对相关知识的理解 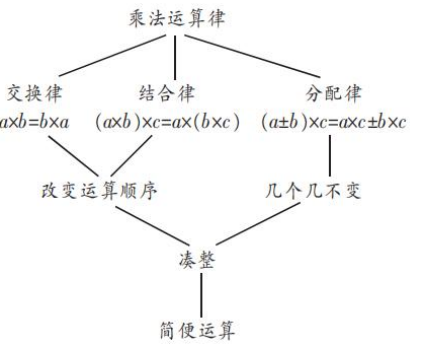
(二)剖析教师课堂展示中的思维导图 以“四则运算”一课的教学为例,教师进行课堂教学时,可通过课堂教学中的“四则运算”定律,引导学生依据自己的思维习惯,进行导图的绘制,培养学生自主学习与梳理知识点的能力。教师可将本章节的数学知识点罗列在黑板上,引导学生依据自己理解方式,利用发散性思维,绘制出可促使其扎实记忆的导图。 在讲解“圆柱与圆锥”相关知识内容时,为了增强学生的空间理解能力,培养学生的空间观念,要采取科学有效的教学方式进行立体几何内容的教学活动。教师可以利用思维导图的方式,将圆柱与圆锥的特征分别向学生进行展示,并引导学生进行想象,在生活中有哪些物体是圆柱体、有哪些物体是圆锥体,让学生学会区分圆柱与圆锥各自的底面、侧面和高。然后通过详细的对比,让学生区分圆柱与圆锥的不同点。在学生了解到圆柱与圆锥存在特征上的差异后,就可以引导学生去探究圆柱与圆锥各自的体积算法。为学生建立清晰的思维导图,可以帮助学生迅速掌握立体几何这种空间概念上的抽象数学。 三、合理整合 将学生优秀的思维导图作品以及教师绘制的模板放在校园四处,拓展学生的视野。利用思维导图加深印象,扩大学习效果。 |
